[Classical Control]Controller Design: Frequency Response

1. Introduction

이번 글에서는 Frequency response에 대해 다룰 것이다. Frequency response의 함수 형태인 Frequency response function부터 이를 그래프 형태로 나타내는 Bode plot, Nyquist plot에 대해 다룰 것이다. Nyquist plot은 특히 Robustness 확보에 중요한 역할을 하는 Plotting 기법이다.

 

2. Frequency Response

Frequency response function은 주어진 Laplace transform을 활용한 Transfer function G(s)의 변수 s를 s=jw 형태로 Real part를 없애고 Imaginary part(주파수 영역)만 고려하는 Transfer function을 말하며 여기서 Fourier transform을 활용한다. 결국 주파수 영역에서 Transfer function의 특성을 보는 것은 Frequency response를 관찰하는 것이다. 따라서 G(s)가 있을 때 Equation 1.과 같이 정의할 수 있다.

Equation 1.

Equation 1.은 Magnitude와 Phase에 따라 Equation 2.과 같이 분리할 수 있다.

Equation 2.

이 때 특정 주파수 w0에 대해 Exponential input을 넣어주면 Steady-state에서의 y(t)를 Equation 3.와 같이 표현할 수 있다.

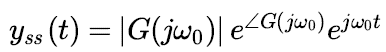
Equation 3.

Euler`s identity에 의해 각 Sinusoidal input에 대해 Equation 4.와 같이 표현할 수 있다.

Equation 4.

이러한 Transfer function을 Frequency response를 통해 찾는 방법은 다음과 같다. 저주파수 10개(예를 들어 w0 = 0.1 ~ 1.0)의 크기를 다음과 같이 찾는다. 입력 u(t)를 입력했을 때, 출력 y(t)는 Equation 5.와 같이 Phase delay와 Magnitude가 바뀌어서 나타난다.

Equation 5.

Figure 1. Frequency Response of System

따라서 Sinusoidal input의 출력을 통해 Transfer function을 Equation 6.처럼 유추하는 것이다. U(s)는 u(t), Y(s)는 y(t)의 Laplace transform이다.

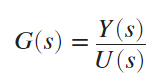
Equation 6.

 

이 과정을 MATLAB의 invfreqs를 통해 역 추론하여 Transfer function을 찾는 과정은 다음과 같다.

n = [9];
d = [1 2 9];
w = logspace(-1,1);

[h,w] = freqs(n,d,w)
[in,id] = invfreqs(h, w, 'complex' , 0, 2)

Figure 2. Result of 'invfreq' in MATLAB

 

3. Bode Plot

위와 같은 Frequency response를 시각화한 것이 바로 Bode plot이다. Bode plot은 Frequency를 Input으로 Magnitude와 Phase plot으로 표현된다. G(jw)가 frequency response function이라고 할 때 이를 Polar equation 형태로 나타내면 Equation 7.과 같다.

Equation 7.

우선은 First-order system에서 Equation 8.과 같이 표현된다. Magnitude는 dB 단위로 Plotting 할 수 있다.

Equation 8.

Stable 한 Second-order system이 실전에서 주로 사용되니 Underdamped system 관점에서만 보면 Equation 9.와 같이 표현할 수 있다.

Equation 9.

위의 수식을 Plot을 그린 것이 Bode plot이다. Bode plot은 특정 Frequency에서 급격하게 Magnitude plot에서 Peak를 찍게 되고, Peak가 되는 Magnitude를 Peak magnitude, 이때의 Frequency를 Resonant frequency라고 하며 Equation 10.과 같이 정의한다.

Equation 10.

앞서 살펴본 예제의 Transfer function을 MATLAB의 Bode 명령어를 통해 Bode plot을 구하면 Figure 3.과 같다.

n = [9];
d = [1 2 9];

H = tf(n,[1 2 9])
bode(H)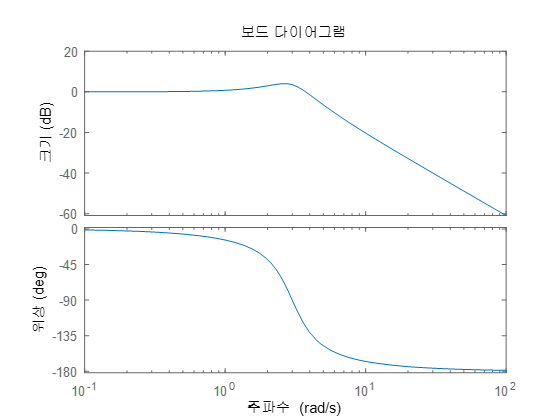

Figure 3. Bode plot of H in MATLAB

 

4. Nyquist Plot

Nyquist plot은 Open-loop frequency response를 통해 Closed-loop system의 Stability와 Transient response, Steady-state error, Robustness를 활용해 설계하는 것에 사용된다. 직접 다루지는 않지만 Root locus의 접근법과도 비슷하다. Figure 4.가 정의되었다고 할 때 각 함수는 Equation 11.과 같이 변환할 수 있다.

Figure 4. Transfer Function

Equation 11.

이를 토대로 Equation 12.를 도출할 수 있다. 여기서 다음과 같은 두가지를 알 수 있다. T(s)는 Closed-loop transfer function이다.

1. Poles of G(s)H(s) = Poles of 1+G(s)H(s)
2. Zeros of 1+G(s)H(s) = Poles of T(s)

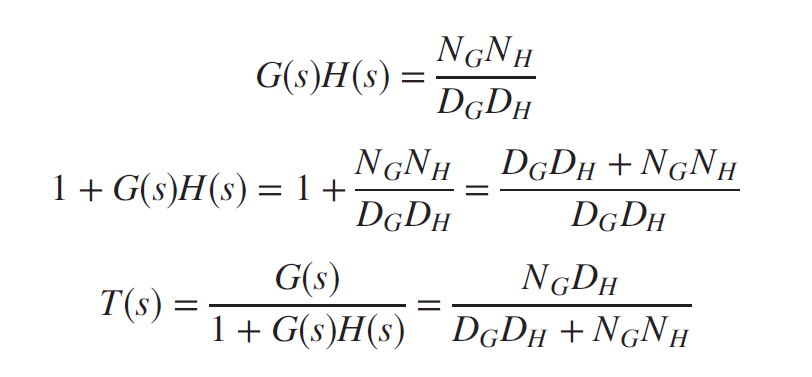
Equation 12.

이를 통해 Mapping을 할 수 있고, 이러한 변형되는 점들의 집합을 Contour라고 부른다.

Equation 13.

Contour A가 존재한다고 할 때, F(s)에 그 값들을 대입해 Contour B로 만들 수 있고 이러한 결과는 Figure 5.처럼 복소수 형태로 Plotting 된다.

Figure 5. Mapping Contour A through function F(s) to Contour B

즉, 각 점들은 F(s)를 통해 특정 복소수 R로 변환되고, R은 Zeros나 Poles의 크기 V를 조합한 형태로 계산된다. 이에 관련한 다양한 예제는 Figure 6.과 같다.

Figure 6. Contour Mapping

여기서 Contour B의 Counterclockwise와 Clockwise 방향을 결정하는 것은 아래 규칙에 의해서 결정된다.

1. Contour A에서 Zero와 Pole이 하나라도 바깥에 있을 때 Contour A의 방향을 따르게 된다.
2. Contour A에서 하나의 Pole과 하나의 Zero만 존재하는 경우 Pole이 있는 Contour B만 Contour A의 반대 방향이 된다.

그렇다면 실제 몇 가지 정리와 예제를 통해 Nyquist plot을 그려보자. 우선 Pure s(s + k 꼴이 아닌 s 그 자체)의 개수를 통해 다음과 같은 규칙으로 시작점이 정해진다. 사분면에 성질에 따라 4주기로 반복된다.

1. 분모 1개 s: -j∞
2. 분모 2개 s: -∞
3. 분모 3개 s: +j∞
4. 분모 4개 s: +∞

또한 N = P(Pole 개수) - Z(Zero 개수)을 통해 다음과 같은 규칙으로 종점이 정해진다. 마찬가지로 사분면에 성질에 따라 4주기로 반복된다.

1. N = 1: -j0
2. N = 2: -0
3. N = 3: +j0
4. N = 4: +0

실제 MATLAB을 통해 Nyquist plot을 그려보며 규칙을 정리해보자.

H = tf([1],[1 2 3])
nyquist(H)

Figure 7. Type 0 Nyquist Plot

위와 같이 Pure s가 없는 Nyquist plot은 +∞ 축에서 시작하여 2 = 2 - 0에 의해 -0으로 수렴하게 된다. Type 1 시스템 예제 한 가지를 더 살펴보자.

H = tf([40],[3 2 3 0])
nyquist(H)

Figure 8. Type 1 Nyquist Plot

위와 같이 Pure s가 1인 Nyquist plot은 -j∞ 축에서 시작하여 3 = 3 - 0에 의해 +j0으로 수렴하게 되는 것을 확인할 수 있다.

 

* Reference

Github Simulation: https://github.com/TitusChoi/Classical_Control/
Figures:
1. Nise, N. S. (2015). Control systems engineering.
2. https://kr.mathworks.com/help/slcontrol/ug/what-is-a-frequency-response-model.html