[Classical Control]Feedback Controller

1. Introduction

실무에서 Feedback은 시스템의 특성을 활용해 Actuator를 만드는 4가지 목적 Efficiency improvement, Stabilization, Elimination of uncertainty, Disturbance rejection을 만족시키기 위한 방법이다. 따라서 이번 포스팅에서는 Feedback을 반영한 Controller의 종류에 대해 알아볼 것이다.

 

2. Feedback Controller

Figure 1. Feedback System

가장 기본적인 Feedback system은 Figure 1.처럼 구성된다. 입력 Reference 값 r(t)와 출력 및 Feedback 값 y(t)의 차이를 오차 e(t)로 정의하고 이를 0으로 만드는 것이 Feedback system의 목적이다. 이때 시스템의 Plant G(s)의 Controller 역할을 하는 C(s)를 Controller라고 하며, Feedback system의 Controller이기 때문에 Feedback controller라고 한다. 이때 H(s)는 y(t)의 상태를 측정하는 Sensor이다. 통상 Sensor는 1로 근사화하여 Feedback 한다. 이 때 Closed-loop Transfer function T(s)을 구하는 과정은 Equation 1.과 같다. 전 과정은 Laplace domain에서 정리되었다.

Equation 1.

 

3. Lead Compensator, Lag Compensator

Lead compensator와 Lag compensator는 Phase margin을 늘려주기 위해 활용하는 Controller이다. 이러한 Compensator의 Transfer function은 Equation 2.와 같다. 입력 X(s)에 대한 출력 Y(s)의 Transfer function은 C(s)이다. zc는 Compensator의 Zero, pc는 Compensator의 Pole이다. 이 때 조건에 따라 Lead, Lag가 나뉜다.

Equation 2.

이러한 Compensator의 Frequency domain에서의 해석을 통해 다음과 같이 Magnitude response와 Phase response를 구할 수 있다.

Equation 3.

이러한 Lead-Lag compensator는 보통 Root locus technique과 같이 쓰인다. 그러나, 실제 현장에서 필자의 경우 Root locus technique을 써본 적이 없기 때문에, 이에 대한 시뮬레이션과 설명은 따로 하지 않도록 하겠다. 간단하게 추가적인 설명을 덧붙여보자면, Frequency response를 통해 Overshoot과 시스템의 Stability를 Lead compensator로 개선할 수 있고, Lag compensator는 Steady-state error를 개선할 수 있다고 한다.

 

4. P Controller, PI Controller, PID Controller

실제 현장에서 90% 이상 사용되고 있는 P Controller, PI Controller, PID Controller에 대해 Figure 2.와 같이 Simulink를 구성하고 살펴보자.

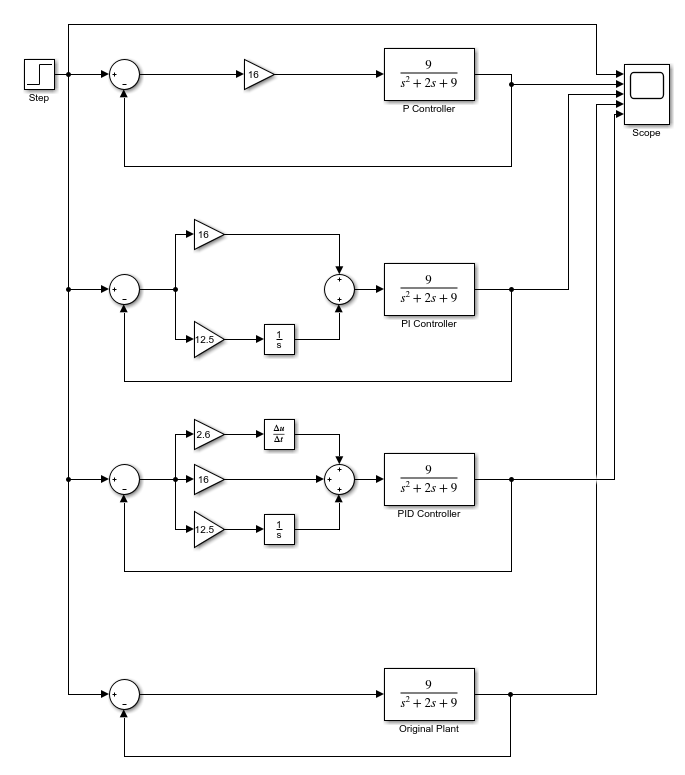
Figure 2. P, PI, PID Controller in Simulink

4.1. P Controller

P Controller는 Proportional gain을 활용하여 Error의 Gain을 높여주는 역할을 하며 추후에 논할 Rising time을 단축시킨다. Reference 값을 추종할 수 있도록 Error와의 차이를 확연히 좁혀준다. 이때 P gain을 kp라고 하면 Controller의 출력 u(t)를 Equation 4.와 같이 표현할 수 있다. 그러나 P Controller를 적용한 Steady-state에서 Error는 0이 되지 않는다.

Equation 4.

이를 전에 활용했던 Transfer function 예제를 활용하여 Figure 3,과 같이 Step response를 구하면 다음과 같은 결과를 얻을 수 있다. Step input과 Controller를 적용하지 않은 Original transfer function과 P Controller를 적용한 경우는 Figure 3.과 같다.

Figure 3. P Controller in Simulink

이를 통해 P Controller는 Error 목표치를 추종할 수 있게 Gain 자체를 조절함을 확인할 수 있다.

4.2. PI Controller

PI Controller는 현장에서 필자가 가장 많이 활용했으며 안정성이 입증된 Controller이다. PI Controller의 Controller 출력u(t)는 Integral gain을 ki라고 할 때 Equation 5.라고 할 수 있다.

Equation 5.

PI Controller와 P Controller의 가장 큰 차이는 Steady-state error이다. PI Controller의 Steady-state error는 0을 추종한다. 이는 FVT(Final Value Theorem)을 통해 증명할 수 있다. 우선 Laplace transform을 활용하여 Equation 6.과 같이 표현할 수 있다.

Equation 6.

이 때 Step response가 R(s)=1/s로 주어지면 결국 PI Controller의 Steady-state error는 0이 됨을 Equation 7.을 보고 확인할 수 있다.

Equation 7.

이를 Simulink를 통해 확인하면 Figure 4.와 같은 결과를 확인할 수 있다. 이러한 PI Controller는 결국 목표 값을 추종하기 때문에 현장에서 가장 많이 활용되는 Controller이다. 주로 Reset 조건을 추가적으로 설정하여 Discrete-time domain에서 설계한다.

Figure 4. PI Controller in Simulink

4.3. PID Controller

PID Controller는 보통 현장에서 Position controller에 활용된다. PID Controller의 Derivative gain은 실제 Digital controller에서 시간이 제대로 전달되지 못해 발산할 가능성이 있기 때문에 주의하여 활용한다. Derivative gain을 포함해서 Equation 8.을 보고 알 수 있다.

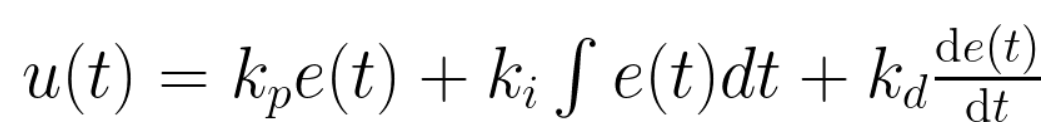
Equation 8.

이는 Laplace transform에서 Equation 9.와 같이 변환된다.

Equation 9.

PID Controller는 PI Controller에 대해 Overshoot과 Oscillation을 줄여주는 효과를 가지고 있으며 Simulink를 통해 확인해보면 Figure 5.와 같다.

Figure 5. PID Controller in Simulink

이러한 P Controller, PI Controller, PID Controller의 각 Gain을 선정하는 과정이 Controller의 Performance를 증가시키는 작업이며, 실제 설계 스펙에 맞게 각 Gain이 선별된다. 실무에서 PID 설계는 PMSM에서 Current controller는 RL 회로의 Pole-zero cancellation을 이용하여 PI gain을 구하고 Position controller의 PID gain은 Pole-placement 기법을 활용하여 선정한다. 그 외의 tuning 기법은 설계 Performance에 대한 기준이 명확하지 않으므로 사용을 자제한다.

 

* Reference

Github Simulation: https://github.com/TitusChoi/Classical_Control/