[Classical Control]Transfer Function_1

1. Introduction

Transfer Function은 앞선 Overview에서 Control system block이며 시스템의 수학적 모델링이라고 했다. 이번에는 최근에 MATLAB과 Simulink를 활용한 Model-based control의 가장 기본이 되는 Transfer function에 대해 알아보기로 하자. 여기에서는 Poles, Zeros, Impulse response, Step response에 대해 다룰 것이다.

[Classical Control]Overview of Control System

 

2. Poles, Zeros

Transfer function G(s)는 Laplace domain의 상수인 s의 비율 함수 형태이다. 이러한 Transfer function을 Equation 1.과 같이 정의할 수 있다.

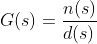
Equation 1.

여기서 n(s)의 다항식 근을 Zero라고 정의하고, 임의의 제로 z0에 대해 Equation 2.과 같이 정의한다.

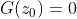
Equation 2.

마찬가지로 d(s)의 다항식 근을 Pole이라고 정의하고, 임의의 폴 p0에 대해 Equation 3.과 같이 정의한다. 또한 d(s)=0인 식을 Characteristic equation이라고 정의한다.

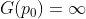
Equation 3.

예를 들어, First-order system이 Equation 4.와 같이 정의되었다고 하자.

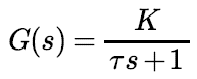
Equation 4.

이 때 시스템의 Pole은 Equation 5.와 같이 정의되며, 이 때 Tau는 Time constant(시정수)로 정의된다.

Equation 5.

이와 함께 Second-order system이 Equation 6.와 같이 Complex poles로 정의되었다고 하자.

Equation 6.

 

이때 Poles는 Equation 7.과 같다.

Equation 7.

특히 Damping ratio와 Natural frequency를 Equation 8.로 정의내리면 Transfer function의 Characteristic equation은 Equation 9.와 같이 Daping ratio와 Natural frequency로 정의내릴 수 있다.

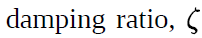
Equation 8.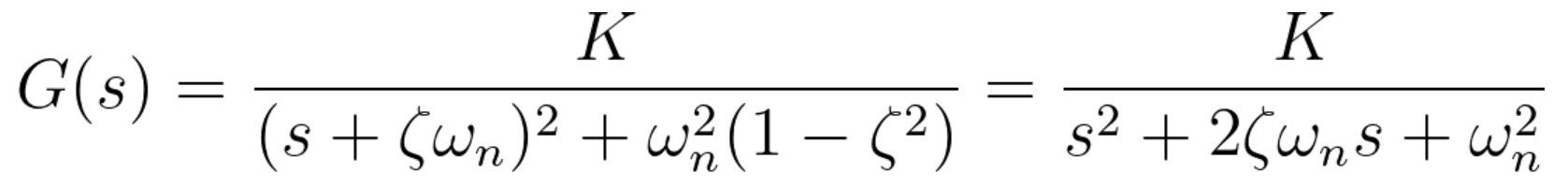

Equation 9.

이때 Poles는 Equation 10.과 같다.

Equation 10.

실제 다음과 같은 Second-order system이 있다고 할 때, MATLAB의 'pzmap' 기능을 활용해서 Pole과 Zero를 확인할 수 있다.

H = tf([5 3],[1 4 10])
pzmap(H)
grid on

Figure 1. PZ Map of H in MATLAB

간단하게 설명했지만, Second-order system은 Figure 2.와 같이 4가지로 나뉜다. 위의 예제는 Underdamped system이다.

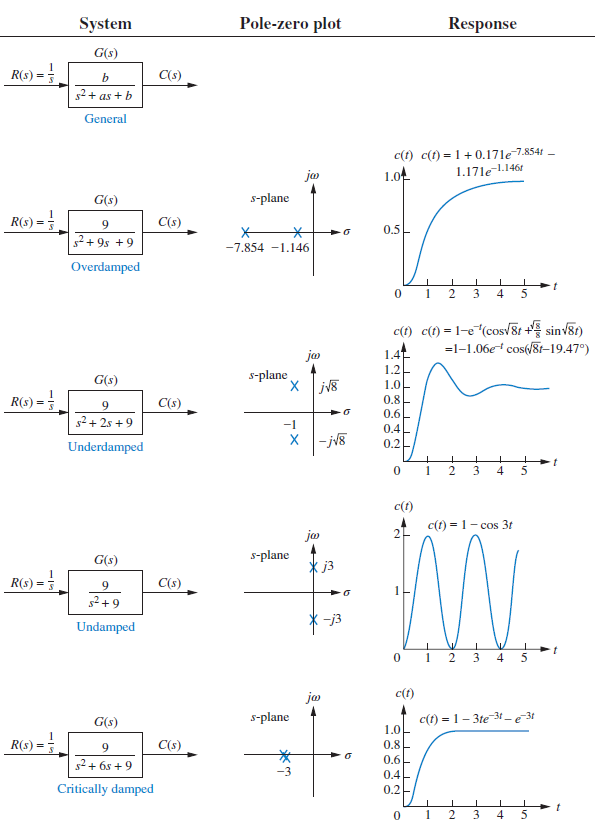
Figure 2. Second-order systems

 

3. Impulse Response(Natural Response)

Time domain에서 가장 간단한 입력으로 특성을 확인할 수 있는 방법 중 하나가 Impulse response이다. 앞선 Introduction에서 시스템의 Total response는 Natural response와 Forced response의 합이라고 했다. Natural response는 시스템의 특성을 보여주는 역할을 한다. 바로 이 특성이 Transfer function이다. Equation 11.이 Unit impulse function의 정의라고 할 때 Impulse response는 시스템의 입력 u(t)를 Unit impulse function으로 줬을 때의 출력 y(s)을 의미한다.

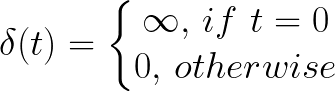
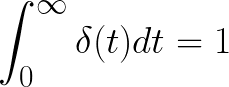
Equation 11.

이때 출력은 Transfer function 그 자체가 된다. 이 관계를 수식으로 풀어보면 Equation 12.가 된다.

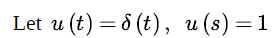
Equation 12.

 

4. Step Response

Impulse response와 마찬가지로 Time domain에서 가장 간단하게 분석할 수 있는 또 다른 방법이 Step response이다.

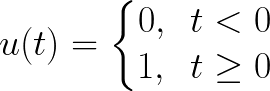
Equation 13.

Equation 13.이 Unit step response의 정의라고 할 때, Step response는 시스템의 입력 u(t)를 Unit step function으로 줬을 때의 출력 y(s)을 의미한다. 이는 Equation 14.처럼 전개된다.

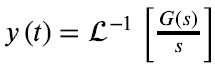
Equation 14.

다음과 같은 Second-order transfer function이 존재한다고 할 때, MATLAB의 'step' 함수를 활용해서 바로 Transfer function의 Step response를 확인할 수 있다.

s = tf('s');
H2 = 1/(s^2+5*s+25)
step(H2)
grid on

Figure 3. Step response of H2 in MATLAB

 

* Reference

Figures & Theories: Nise, N. S. (2015). Control systems engineering.
Github Simulation: https://github.com/TitusChoi/Classical_Control/
MATLAB Models: https://kr.mathworks.com/help/control/ref/lti.step.html;jsessionid=51fd65401e0b849296475ec46c25